Phase transitions in large language models ..
.. and a bold prediction
Have you wondered why the leading players in the field of AI try to make models larger, larger and larger? It somehow resembles what happened in astronomy in ancient India building ever larger observatories and what has been happening in particle physics since the middle of the last century: Building larger and larger machines to discover new properties of matter by using more and more energy to accelerate the colliding particles and hence “going up on the energy scale.” Sometimes the motivation was to confirm theoretical predictions and sometimes there were surprising discoveries to be made by pushing the boundaries of what can be observed.
One, if not the main reason, why a similar trend happens in AI, is that a most remarkable thing happens when making large models larger and larger: The models exhibit properties that they were not trained to obtain. Foundation models behind a large language model are typically trained to predict the next word (token) in a sentence. For instance, to predict the word “yellow” in “The color of a banana is _____.” And suddenly, when the model gets big enough, it is able to do new things, for instance solving basic math problems or logic puzzles. Such behaviour has been discovered several years ago and termed “emerging abilities”. If you would like to understand a bit more in depth why such things occur, I recommend reading Jason Wei’s blog post on the matter [1].
Predicting the properties of large language models with growing size has been a field of active research for the last couple of years. It has been quite successfully and culminated in so-called “scaling laws”. Briefly speaking, scaling laws allows to predict how well large language models perform on particular tasks when we scale them up. Scaling in this context means - increasing the amount of parameters in a model, the amount of data that the model was trained on and the total training time (without changing the model’s general architecture).
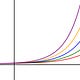
A convenient way to describe scaling laws is by using the total compute that was used to train it in FLOPs (floating point operations) and looking at the performance on particular tasks depending on the total amount of compute that went into training the model. This is shown in the Figure below for 8 different tasks. The figure was taken from [2].
While reading the paper and seeing these graphs, two thoughts sparkled instantly into my physicist mind:
1) The plots remind me a lot of typical plots that we see for phase transition in materials, e.g. the R(T) curve of superconductors. It is quite exciting that these models seem to exhibit similarities to what we know from statistical physics. As a higher level of order in materials allows for new properties to emerge, it seems that a higher level of information and information compression allows new properties to emerge in these models.
2) I am not sure if it is just a coincidence due to the architecture of the particular models that have been used but I find it very interesting that these emerging properties or “phase transitions”, seem to occur at an order of magnitude around 10^23, i.e. around the value of the Avogadro constant.
While it might seem a very naïve and speculative claim, one could think that human-like intelligence might appear when we reach around 10^26 to 10^27 FLOPs of model scale (which would correspond roughly to the number of atoms in the human brain). This number is not that far off anymore as it’s estimated that ChatGPT was trained with about 10^25 FLOPs. Interestingly, about two orders of magnitude is also the ratio between the number of parameters in ChatGPT-4 and an estimate on how many “parameters” a human brain might have (roughly 10^27).
Leaving aside interesting observations and going back to scaling laws: Scaling laws have the nice property that they make a very easy and tangible connection between “how much compute, hence money, I have to invest” and “what outcome can I expect”. And this might give us a vague explanation why you have seen headlines in the press like “Sam Altman is looking to raise $5T from investors”.
If $10B have went into training a model with 10^25 FLOPs and you need to scale by two orders of magnitude to get to human-like intelligence, you need about two orders of magnitude more of investment to cover the corresponding costs if the price per FLOP is not expected to drop significantly over the next years.
[1] https://www.jasonwei.net/blog/some-intuitions-about-large-language-models
[2] https://arxiv.org/abs/2211.02011